जब यह आता हैएंटेनालोगों के मन में सबसे ज्यादा चिंता इस बात को लेकर है कि "विकिरण वास्तव में कैसे उत्पन्न होता है?" सिग्नल स्रोत द्वारा उत्पन्न विद्युत चुम्बकीय क्षेत्र ट्रांसमिशन लाइन और एंटीना के अंदर कैसे फैलता है, और अंत में एंटीना से "अलग" होकर मुक्त अंतरिक्ष तरंग कैसे बनाता है?
1. एकल तार विकिरण
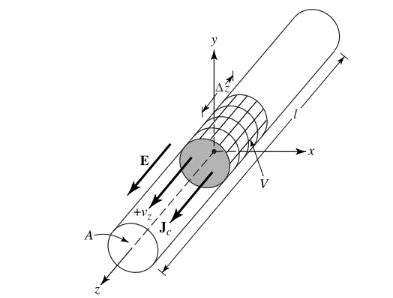
मान लीजिए कि आवेश घनत्व, जिसे qv (कूलम्ब/m³) के रूप में व्यक्त किया जाता है, एक वृत्ताकार तार में समान रूप से वितरित है जिसका अनुप्रस्थ काट क्षेत्रफल a और आयतन V है, जैसा कि चित्र 1 में दिखाया गया है।
चित्र 1
आयतन V में कुल आवेश Q, z दिशा में एकसमान गति Vz (m/s) से गति करता है। यह सिद्ध किया जा सकता है कि तार के अनुप्रस्थ काट पर धारा घनत्व Jz निम्न है:
Jz = qv vz (1)
यदि तार एक आदर्श चालक से बना है, तो तार की सतह पर धारा घनत्व Js होगा:
Js = qs vz (2)
जहां qs सतह आवेश घनत्व है। यदि तार बहुत पतला है (आदर्श रूप से, त्रिज्या 0 है), तो तार में धारा को इस प्रकार व्यक्त किया जा सकता है:
Iz = ql vz (3)
जहां ql (कूलम्ब/मीटर) प्रति इकाई लंबाई का आवेश है।
हम मुख्य रूप से पतले तारों से संबंधित हैं, और निष्कर्ष उपरोक्त तीनों मामलों पर लागू होते हैं। यदि धारा समय के साथ बदलती रहती है, तो सूत्र (3) का समय के सापेक्ष अवकलन इस प्रकार है:
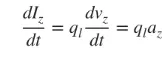
(4)
az आवेश त्वरण है। यदि तार की लंबाई l है, तो (4) को इस प्रकार लिखा जा सकता है:
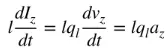
(5)
समीकरण (5) धारा और आवेश के बीच मूलभूत संबंध है, और विद्युत चुम्बकीय विकिरण का भी मूलभूत संबंध है। सरल शब्दों में, विकिरण उत्पन्न करने के लिए, समय के साथ बदलती धारा या आवेश का त्वरण (या मंदन) होना आवश्यक है। हम आमतौर पर समय-सामंजस्यपूर्ण अनुप्रयोगों में धारा का उल्लेख करते हैं, और आवेश का उल्लेख अक्सर क्षणिक अनुप्रयोगों में किया जाता है। आवेश त्वरण (या मंदन) उत्पन्न करने के लिए, तार को मोड़ा, तह किया और असंतत होना चाहिए। जब आवेश समय-सामंजस्यपूर्ण गति में दोलन करता है, तो यह आवधिक आवेश त्वरण (या मंदन) या समय के साथ बदलती धारा भी उत्पन्न करेगा। इसलिए:
1) यदि आवेश गति नहीं करता है, तो कोई धारा और कोई विकिरण नहीं होगा।
2) यदि आवेश स्थिर गति से गति करता है:
ए. यदि तार सीधा और अनंत लंबाई का हो, तो कोई विकिरण नहीं होता है।
बी. यदि तार मुड़ा हुआ, तह किया हुआ या असंतुलित है, जैसा कि चित्र 2 में दिखाया गया है, तो विकिरण होता है।
3) यदि आवेश समय के साथ दोलन करता है, तो तार सीधा होने पर भी आवेश विकिरण करेगा।
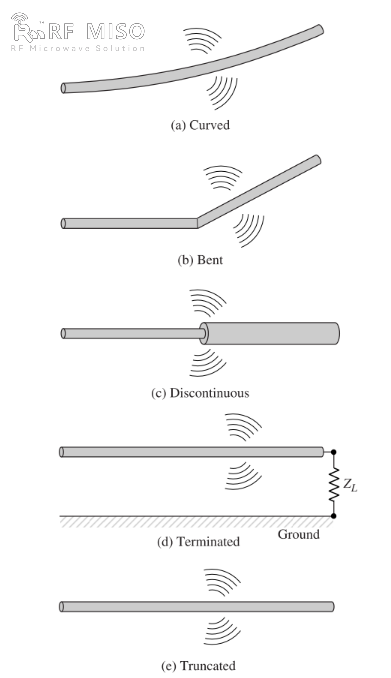
चित्र 2
विकिरण क्रियाविधि की गुणात्मक समझ प्राप्त करने के लिए, एक स्पंदित स्रोत को एक खुले तार से जोड़ा जा सकता है, जिसे उसके खुले सिरे पर भार के माध्यम से ग्राउंड किया जा सकता है, जैसा कि चित्र 2(d) में दिखाया गया है। जब तार को प्रारंभ में ऊर्जा दी जाती है, तो स्रोत द्वारा उत्पन्न विद्युत क्षेत्र रेखाओं के कारण तार में मौजूद आवेश (मुक्त इलेक्ट्रॉन) गति में आ जाते हैं। जैसे ही आवेश तार के स्रोत वाले सिरे पर त्वरित होते हैं और उसके सिरे पर परावर्तित होने पर मंदित (मूल गति के सापेक्ष ऋणात्मक त्वरण) होते हैं, इसके सिरों पर और तार के शेष भाग में एक विकिरण क्षेत्र उत्पन्न होता है। आवेशों का त्वरण एक बाह्य बल स्रोत द्वारा होता है जो आवेशों को गति प्रदान करता है और संबंधित विकिरण क्षेत्र उत्पन्न करता है। तार के सिरों पर आवेशों का मंदन प्रेरित क्षेत्र से जुड़े आंतरिक बलों द्वारा होता है, जो तार के सिरों पर केंद्रित आवेशों के संचय के कारण उत्पन्न होता है। आंतरिक बल आवेश के संचय से ऊर्जा प्राप्त करते हैं क्योंकि तार के सिरों पर उनका वेग शून्य हो जाता है। इसलिए, विद्युत क्षेत्र उत्तेजना के कारण आवेशों का त्वरण और तार प्रतिबाधा की असंतुलन या समतल वक्रता के कारण आवेशों का मंदन, विद्युत चुम्बकीय विकिरण उत्पन्न करने वाले तंत्र हैं। यद्यपि धारा घनत्व (Jc) और आवेश घनत्व (qv) दोनों मैक्सवेल के समीकरणों में स्रोत पद हैं, आवेश को अधिक मौलिक मात्रा माना जाता है, विशेष रूप से क्षणिक क्षेत्रों के लिए। यद्यपि विकिरण की यह व्याख्या मुख्य रूप से क्षणिक अवस्थाओं के लिए उपयोग की जाती है, इसका उपयोग स्थिर-अवस्था विकिरण की व्याख्या करने के लिए भी किया जा सकता है।
कई बेहतरीन विकल्पों की अनुशंसा करता हूँ।एंटीना उत्पादद्वारा निर्मितआरएफएमआईएसओ:
2. दो-तार विकिरण
चित्र 3(a) में दिखाए अनुसार, एक एंटीना से जुड़ी दो-चालक संचरण रेखा में एक वोल्टेज स्रोत जोड़ें। दो-तार वाली रेखा पर वोल्टेज लगाने से चालकों के बीच एक विद्युत क्षेत्र उत्पन्न होता है। विद्युत क्षेत्र रेखाएं प्रत्येक चालक से जुड़े मुक्त इलेक्ट्रॉनों (परमाणुओं से आसानी से अलग होने वाले) पर क्रिया करती हैं और उन्हें गतिमान होने के लिए बाध्य करती हैं। आवेशों की गति से धारा उत्पन्न होती है, जो बदले में एक चुंबकीय क्षेत्र उत्पन्न करती है।
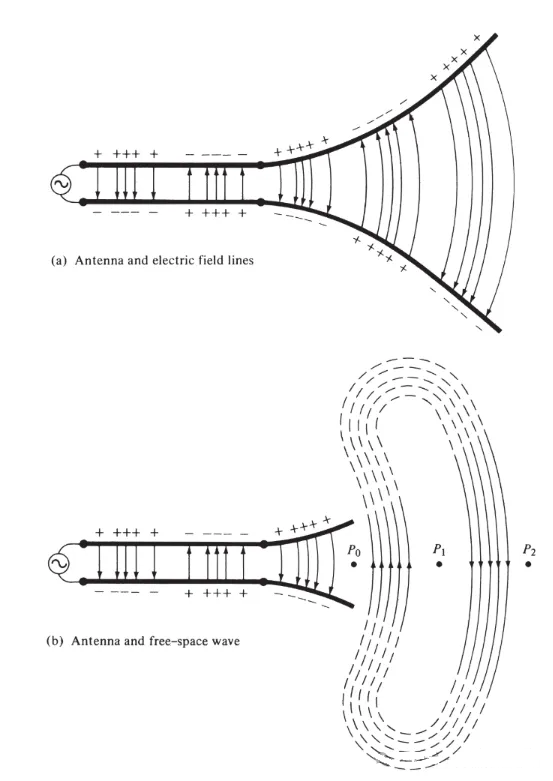
चित्र तीन
हमने यह मान लिया है कि विद्युत क्षेत्र रेखाएँ धनात्मक आवेशों से शुरू होकर ऋणात्मक आवेशों पर समाप्त होती हैं। बेशक, वे धनात्मक आवेशों से शुरू होकर अनंत पर भी समाप्त हो सकती हैं; या अनंत से शुरू होकर ऋणात्मक आवेशों पर समाप्त हो सकती हैं; या ऐसे बंद लूप बना सकती हैं जो किसी भी आवेश से शुरू या समाप्त नहीं होते। चुंबकीय क्षेत्र रेखाएँ हमेशा धारा प्रवाहित करने वाले चालकों के चारों ओर बंद लूप बनाती हैं क्योंकि भौतिकी में कोई चुंबकीय आवेश नहीं होते। कुछ गणितीय सूत्रों में, समतुल्य चुंबकीय आवेशों और चुंबकीय धाराओं को शक्ति और चुंबकीय स्रोतों से संबंधित समाधानों के बीच द्वैतता दर्शाने के लिए शामिल किया जाता है।
दो चालकों के बीच खींची गई विद्युत क्षेत्र रेखाएँ आवेश के वितरण को दर्शाती हैं। यदि हम मान लें कि वोल्टेज स्रोत साइनसोइडल है, तो चालकों के बीच विद्युत क्षेत्र भी साइनसोइडल होगा और उसका आवर्तकाल स्रोत के आवर्तकाल के बराबर होगा। विद्युत क्षेत्र की सापेक्ष तीव्रता को विद्युत क्षेत्र रेखाओं के घनत्व द्वारा दर्शाया जाता है, और तीर सापेक्ष दिशा (धनात्मक या ऋणात्मक) को इंगित करते हैं। चालकों के बीच समय-परिवर्ती विद्युत और चुंबकीय क्षेत्रों के उत्पन्न होने से एक विद्युत चुम्बकीय तरंग बनती है जो संचरण रेखा के अनुदिश प्रसारित होती है, जैसा कि चित्र 3(a) में दिखाया गया है। विद्युत चुम्बकीय तरंग आवेश और संबंधित धारा के साथ एंटीना में प्रवेश करती है। यदि हम एंटीना संरचना के एक भाग को हटा दें, जैसा कि चित्र 3(b) में दिखाया गया है, तो विद्युत क्षेत्र रेखाओं के खुले सिरों (बिंदीदार रेखाओं द्वारा दर्शाए गए) को "जोड़कर" एक मुक्त-स्थान तरंग बनाई जा सकती है। मुक्त-स्थान तरंग भी आवर्तकाल वाली होती है, लेकिन स्थिर-चरण बिंदु P0 प्रकाश की गति से बाहर की ओर गति करता है और आधे आवर्तकाल में λ/2 (P1 तक) की दूरी तय करता है। एंटेना के पास, स्थिर-चरण बिंदु P0 प्रकाश की गति से तेज़ गति से चलता है और एंटेना से दूर बिंदुओं पर प्रकाश की गति के करीब पहुँच जाता है। चित्र 4, t = 0, t/8, t/4 और 3T/8 पर λ/2 एंटेना के मुक्त-स्थान विद्युत क्षेत्र वितरण को दर्शाता है।
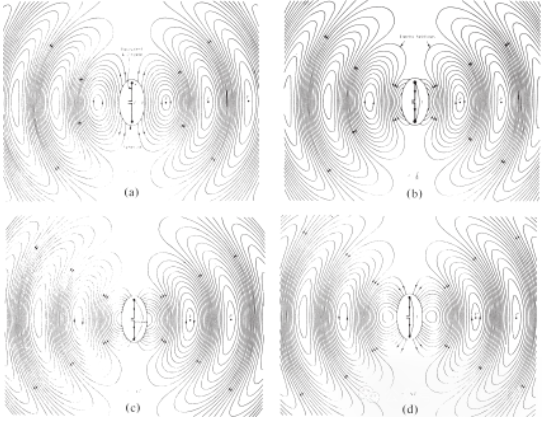
चित्र 4 t = 0, t/8, t/4 और 3T/8 पर λ/2 एंटीना का मुक्त स्थान विद्युत क्षेत्र वितरण दर्शाता है।
यह ज्ञात नहीं है कि निर्देशित तरंगें एंटीना से कैसे अलग होती हैं और अंततः मुक्त अंतरिक्ष में फैलने के लिए कैसे बनती हैं। हम निर्देशित और मुक्त अंतरिक्ष तरंगों की तुलना जल तरंगों से कर सकते हैं, जो शांत जल में पत्थर गिराने या अन्य तरीकों से उत्पन्न हो सकती हैं। जल में हलचल शुरू होते ही जल तरंगें उत्पन्न होती हैं और बाहर की ओर फैलने लगती हैं। हलचल रुकने पर भी तरंगें नहीं रुकतीं बल्कि आगे बढ़ती रहती हैं। यदि हलचल बनी रहती है, तो लगातार नई तरंगें उत्पन्न होती रहती हैं, और इन तरंगों का प्रसार अन्य तरंगों से पीछे रह जाता है।
विद्युत विक्षोभ से उत्पन्न विद्युतचुंबकीय तरंगों के लिए भी यही सत्य है। यदि स्रोत से प्रारंभिक विद्युत विक्षोभ अल्पकालिक होता है, तो उत्पन्न विद्युतचुंबकीय तरंगें संचरण रेखा के भीतर फैलती हैं, फिर एंटीना में प्रवेश करती हैं, और अंत में मुक्त स्थान तरंगों के रूप में विकीर्ण होती हैं, भले ही उत्तेजना अब मौजूद न हो (ठीक वैसे ही जैसे जल तरंगें और उनके द्वारा उत्पन्न विक्षोभ)। यदि विद्युत विक्षोभ निरंतर होता है, तो विद्युतचुंबकीय तरंगें निरंतर बनी रहती हैं और प्रसार के दौरान उनके ठीक पीछे चलती हैं, जैसा कि चित्र 5 में दिखाए गए द्विशंक्वाकार एंटीना में दर्शाया गया है। जब विद्युतचुंबकीय तरंगें संचरण रेखाओं और एंटीना के भीतर होती हैं, तो उनका अस्तित्व चालक के भीतर विद्युत आवेश के अस्तित्व से संबंधित होता है। हालांकि, जब तरंगें विकीर्ण होती हैं, तो वे एक बंद परिपथ बनाती हैं और उनके अस्तित्व को बनाए रखने के लिए कोई आवेश नहीं होता है। इससे हम इस निष्कर्ष पर पहुंचते हैं कि:
क्षेत्र की उत्तेजना के लिए आवेश के त्वरण और मंदन की आवश्यकता होती है, लेकिन क्षेत्र को बनाए रखने के लिए आवेश के त्वरण और मंदन की आवश्यकता नहीं होती है।
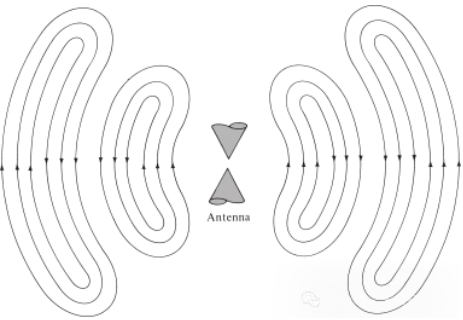
चित्र 5
3. द्विध्रुवीय विकिरण
हम उस प्रक्रिया को समझाने का प्रयास करते हैं जिसके द्वारा विद्युत क्षेत्र रेखाएँ एंटीना से अलग होकर मुक्त-स्थान तरंगें बनाती हैं, और इसके लिए हम द्विध्रुव एंटीना का उदाहरण लेते हैं। यद्यपि यह एक सरलीकृत व्याख्या है, फिर भी इससे लोग मुक्त-स्थान तरंगों के निर्माण को सहज रूप से समझ पाते हैं। चित्र 6(a) में द्विध्रुव की दोनों भुजाओं के बीच उत्पन्न विद्युत क्षेत्र रेखाएँ दर्शाई गई हैं, जब चक्र के पहले चौथाई भाग में विद्युत क्षेत्र रेखाएँ λ/4 की दूरी तक बाहर की ओर गति करती हैं। इस उदाहरण के लिए, मान लें कि निर्मित विद्युत क्षेत्र रेखाओं की संख्या 3 है। चक्र के अगले चौथाई भाग में, मूल तीन विद्युत क्षेत्र रेखाएँ λ/4 की दूरी तक (प्रारंभिक बिंदु से कुल λ/2 की दूरी तक) गति करती हैं, और चालक पर आवेश घनत्व घटने लगता है। इसे विपरीत आवेशों के प्रवेश के कारण उत्पन्न माना जा सकता है, जो चक्र के पहले आधे भाग के अंत में चालक पर मौजूद आवेशों को रद्द कर देते हैं। विपरीत आवेशों द्वारा उत्पन्न विद्युत क्षेत्र रेखाएँ 3 हैं और λ/4 की दूरी तक गति करती हैं, जिसे चित्र 6(b) में बिंदीदार रेखाओं द्वारा दर्शाया गया है।
अंततः, पहले λ/4 दूरी में तीन नीचे की ओर विद्युत क्षेत्र रेखाएँ और दूसरे λ/4 दूरी में उतनी ही ऊपर की ओर विद्युत क्षेत्र रेखाएँ होती हैं। चूंकि एंटीना पर कोई शुद्ध आवेश नहीं है, इसलिए विद्युत क्षेत्र रेखाओं को चालक से अलग होकर आपस में जुड़कर एक बंद परिपथ बनाना पड़ता है। इसे चित्र 6(c) में दर्शाया गया है। दूसरे भाग में भी यही भौतिक प्रक्रिया दोहराई जाती है, लेकिन ध्यान दें कि दिशा विपरीत होती है। इसके बाद, प्रक्रिया दोहराई जाती है और अनिश्चित काल तक जारी रहती है, जिससे चित्र 4 के समान विद्युत क्षेत्र वितरण बनता है।
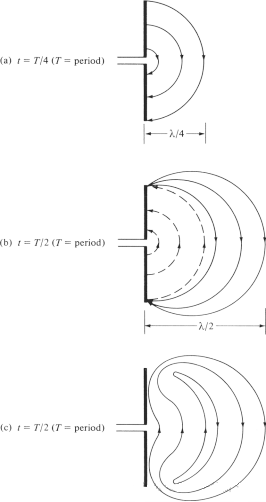
चित्र 6
एंटेना के बारे में अधिक जानने के लिए, कृपया यहां जाएं:
पोस्ट करने का समय: 20 जून 2024










